haabazaar.blogg.se - Algebra 1 factoring trinomials worksheet 5xsquare

Question 1: Which of the following is a binomial?Ĭ)3a*4b* 2c will give 24abc, which is a monomial Standard Identities of Binomials and Trinomials.When an nth-degree of single-variable polynomial equals to 0, then the resultant polynomial equation of degree ‘n’ acquires the following form:Ī nx n + a n-1x n-1 + … + a 2x 2 + a 1x + a = 0īrowse more Topics under Algebraic Expressions And Identities Therefore, the above expression can be shortened to:Ī nx n + a n-1x n-1 + … + a 2x 2 + a 1x + a Since x 1 = x and x 0 = 1 considering all complex numbers x. In this, a’s denote the coefficients whereas x denotes the variable. Since the highest exponent is 1, the degree of 7x – 5 is also 1.Ī single-variable polynomial having degree n has the following equation:Ī nx n + a n-1x n-1 + … + a 2x 2 + a 1x 1 + a 0x 0

The exponent for the first term 7x is 1 and for the second term -5, it is 0. Now, let us define the exponent for each term. In the given example, the first term is 7x, whereas the second term is -5. It is simply the greatest of the exponents or powers over the various terms present in the algebraic expression. For example: 0x 2 + 0x – 0 Degree of a Polynomial In this type, the value of every coefficient is zero. There is another type of polynomial called the zero polynomial. Likewise, 12pq + 4x 2 – 10 is a trinomial. It is due to the presence of three, unlike terms, namely, 3x, 5x 2 and 6x 3. For example- 3x + 5x 2 – 6x 3 is a trinomial. Trinomials – Trinomials are the algebraic expressions with three unlike terms, hence the name “Tri”nomial.

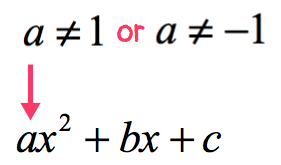
For example, 3x + 4x 2 is binomial since it contains two unlike terms, that is, 3x and 4x 2.

Binomials – Binomials are the algebraic expressions with two unlike terms, hence the name “Bi”nomial.

Furthermore, 4t, 21x 2y, 9pq etc are monomials because each of these expressions contains only one term. For example, 2x + 5x + 10x is a monomial because when we add the like terms it results in 17x. In other words, it is an expression that contains any count of like terms.

Monomials – Monomials are the algebraic expressions with one term, hence the name “Mono”mial.

It will form the base to further learning. Let us get familiar with the different types of polynomials. Amusingly, the simplest polynomials hold one variable. In simple words, polynomials are expressions comprising a sum of terms, where each term holding a variable or variables is elevated to power and further multiplied by a coefficient.